Circuit & Field Theory - short answer questions from AMIE exams (Winter 2019)

on
Explain the following terms in brief

Superposition theorem with a suitable circuit diagram.
Superposition theorem states that in any linear, bilateral network where more than one source is present, the response across any element in the circuit, is the sum of the responses obtained from each source considered separately while all other sources are replaced by their internal resistance. Superposition theorem is a circuit analysis theorem that is used to solve the network where two or more sources are present and connected.
The application of this theorem is both the AC & DC circuits where it assists to build the circuits like “Norton” as well as “Thevenin” equivalent circuits.

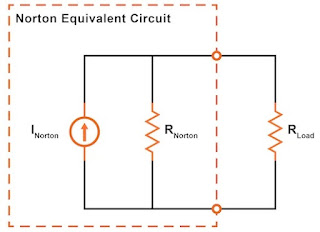
Norton’s theorem with a suitable circuit diagram.
Norton’s Theorem states that it is possible to simplify any linear circuit, no matter how complex, to an equivalent circuit with just a single current source and parallel resistance connected to a load. 
 
 
Coulomb’s law and Biot-Savart’s law
Coulomb’s Law.  Coulomb stated that the force between two very small objects separated in a vacuum by a distance that is large compared to their size is proportional to the charge on each and inversely proportional to the square of the distance between them, or

Where, 
Q1, Q2   = positive or negative charges (C, Coulomb)
R = separation            
ε0 = permittivity of free space( F/m, Farad/meter)
 
Biot-Savart's Law
Biot-Savart’s law is an equation that gives the magnetic field produced due to a current-carrying segment. This segment is taken as a vector quantity known as the current element. The Biot Savart law is fundamental to magnetostatics, playing a role similar to that of Coulomb’s law in electrostatics.

 

 
It is given by the following equation

Equipotential surface with an example
Electric potential is the potential energy per unit charge. Potential on an equipotential surface is constant through the surface. The direction of the electric field is perpendicular to the equipotential surface.

At every point on the equipotential surface, electric field lines are perpendicular to the surface. This is because potential gradient along any direction parallel to the surface is zero i.e.,
E = - (dv/dr) = 0
so component of electric Field parallel to equipotential surface is zero.

The transfer function of a system with its limitation
A transfer function is expressed as the ratio of the Laplace transform of output to the Laplace transform of input assuming all initial conditions to be zero.
Consider a system whose time-domain block diagram is

Time-domain

where, r(t) = input and c(t) = output

Now taking Laplace transform then

Laplace domain


Now the transfer function G(s) is given by
G(s) = C(s)/R(s)

Disadvantages of Transfer function
  • The transfer function does not take into account the initial conditions.
  • The transfer function can be defined for linear systems only.
  • No inferences can be drawn about the physical structure of the system.
---
The study material for AMIE/B Tech/Junior Engineer exams is available at https://amiestudycircle.com



Comments

Post a Comment