Design of Machine Elements - short answer type Questions from AMIE exams (Summer 2018)

Answer the following questions briefly.

Torsional rigidity and lateral rigidity

Torsional Rigidity

Torsional rigidity is the resistance against torsional deformation. Or the minimum force required to deform the object by twisting. It is the product of modulus of rigidity(G) and polar moment of inertia (J), denoted by k, having S.I. Units N.m²

It is given by

$\frac{L}{{GJ}} = \frac{1}{{torsional\,stiffness}}$

Lateral rigidity

Lateral rigidity is the resistance against the bending deformation .or the minimum force required to deform the object by bending. It is represented by EI.

Surface Hardening

A number of components require only a hard surface to resist wear and tear and a tough core to resist shock loads instead of the complete component being made hard. These two properties do not exist in one steel. For toughness, one finds that the core should not exceed 0.3% carbon content, also sometimes it is not desirable to harden the complete components. For example, it is undesirable to have case-harden screw threads. The threads would be brittle and distortion during hardening would need expensive thread grinding operations to correct the distortions. Surface hardening is classified into two types:

Following are the techniques of surface hardening:

Flame hardening
Induction hardening
Laser hardening
Electron beam hardening

Petroff Equation

Petroff’s equation is used to determine the coefficient of friction in journal bearings. Petroff’s equation is important because it defines the group of dimensionless parameters that govern the frictional properties of the bearing.

This equation is given by

$f = (2{\pi ^2})\left( {\frac{r}{c}} \right)\left( {\frac{{\mu {n_s}}}{p}} \right)$

The efficiency of a Riveted Joint

The efficiency of the riveted joint is defined as the ratio of the strength of riveted joint to the strength of the unriveted solid plate. The strength of the riveted joint is the lowest value of P_s P_t and P_c. The strength of solid plate of width, equal to the pitch p and thickness t, subjected to tensile stress is given by,

P = ptσ_t

Therefore, the efficiency is given by,

$\eta = \frac{{Lowest\,of\,{P_s},{P_t}\,\& \,{P_c}}}{P}$

where

P_s = shear resistance of rivet per pitch length (N)

Pt = tensile resistance of plate per pitch length (N)

Pc = crushing resistance of plate per pitch length (N)

Tolerance and Fit

Tolerance

Tolerance is defined as the permissible variation in the dimensions of the component. The two limits are

sometimes called the upper and lower deviations.

There are two systems of specification for tolerances, namely, unilateral and bilateral.

In the unilateral system, one tolerance is zero, while the other takes care of all permissible variations in basic size.
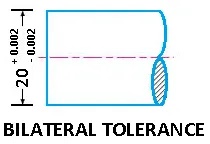
In the case of bilateral tolerances, the variations are given in both directions from normal size. The upper limit, in this case, is the basic size plus non-zero positive tolerance and the lower limit is the basic size plus non-zero negative tolerance.

Fit

When two parts are to be assembled, the relationship resulting from the difference between their sizes before assembly is called a fit. Depending upon the limits of the shaft and the hole, fits are broadly classified into three groups—clearance fit, transition fit and interference fit.

A clearance fit is a fit that always provides a positive clearance between the hole and the shaft over the entire range of tolerances. In this case, the tolerance zone of the hole is entirely above that of the shaft. An interference fit is a fit that always provides a positive interference over the whole range of tolerances. In this case, the tolerance zone of the hole is completely below that of the shaft. A transition fit is a fit that may provide either a clearance or interference, depending upon the actual values of the individual tolerances of the mating components. In this case, the tolerance zones of the hole and the shaft overlap.

Notch Sensitivity

It is the measure of how sensitive a material is, towards the notches or geometric discontinuities. Numerically it is given by the ratio of increase in actual stress over nominal stress with an increase in theoretical stress over nominal stress. These increases in stress are due to stress concentration.

Design of Compression and Extension Springs

There are two basic types of helical springs—compression spring (figure a) and extension spring (figure b).

In helical compression spring, the external force tends to shorten the spring. In helical extension spring, the external force tends to lengthen the spring.

There are two basic equations for the design of helical springs, viz., load-stress equation and load-deflection equation.

Consider following figure

The torsional shear stress in the bar is given by,

$\tau = {K_s}\left( {\frac{{8PD}}{{\pi {d^3}}}} \right)$

where ${K_s}$ is shear stress correction factor.

An equivalent bar is shown below.

The angle of twist (θ) for the equivalent bar is

$\theta = \frac{{{M_t}l}}{{JG}}$

where,

θ = angle of twist (radians)

M_t = torsional moment (PD/2)

l = length of bar (πDN)

J = polar moment of inertia of bar (πd⁴/32)

G = modulus of rigidity

This equation finally becomes

$\theta = \frac{{16P{D^2}N}}{{G{d^4}}}$

Load deflection equation is given as

$\delta = \frac{{8P{D^3}N}}{{G{d^4}}}$

Condition for full film lubrication

Hydrodynamic or full film lubrication is the condition when the load carrying surfaces are separated by a relatively thick film of lubricant. This is a stable regime of lubrication and metal to metal contact does not occur during the steady state operation of the bearing. The lubricant pressure is self generated by the moving surfaces drawing the lubricant into the wedge formed by the bounding surfaces at a high enough velocity to generate the pressure to completely separate the surfaces and support the applied load.

This lubrication regime condition occurs after a machine has begun to rotate and the speeds and loads are such that a wedge of oil has been formed between the shaft and bearing surfaces. This wedge of oil lifts the shaft away from the bearing surface so there is little risk of asperity contact. This is a desirable condition to avoid friction and wear.

Any friction remaining is found within the lubricant itself, as the molecular structures of the oil slide past each other during operation.

Membrane Stresses

It is Average stress value across the thickness of a solid section, excluding the effects of discontinuities and stress concentrations.

Membrane stress in a section is the average stress induced by a force normal to the section. It is calculated using the classical equation for normal stress (S = F/A).

Condition for full lubrication

Already answered.

---

The study material for AMIE/B Tech/Junior Engineer exams is available at https://amiestudycircle.com

AMIE Study Circle Blog

Search This Blog