Skip to main content

Mechanics of Solids - MCQ from AMIE Exams (AMIE Summer 2018)

Choose the correct answer in the following questions (10 x 2)

1. There is always a limiting value of load up to which strain is totally disappeared on the removal of load, the stress corresponding to this load is called as:
(a) Elastic limit
(b) Unit stress
(c) Yield stress
(d) Ultimate stress

2. In a two-dimensional stress system the maximum shear stress occurs on planes inclined with horizontal as:
(a) \frac{1}{2}{\tan ^{ - 1}}\frac{{2{\tau _{xy}}}}{{{\sigma _x} - {\sigma _y}}}
(b) \frac{1}{2}{\tan ^{ - 1}}\frac{{{\sigma _x} - {\sigma _y}}}{{2{\tau _{xy}}}}
(c) 90⁰
(d) 0°

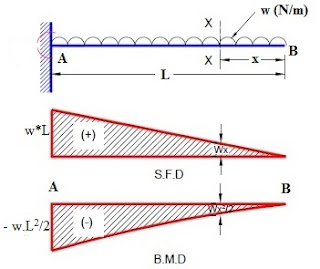
3. In a cantilever beam with a uniformly distributed load, the shear force varies as
(a) linear laws
(b) parabolic law
(c) cubic law
(d) constant, does not vary

4. The diameter of the kernel of a circular section (no tension) is
(a) d/2
(b) d/3
(c) d/4
(d) d/√2

5. The amount of deflection of a beam subject to some type of loading depends on :
(a) cross section
(b) bending moment
(c) either (a) or (b)
(d) both (a) and (b)

6. A pipe of 200 mm internal diameter and 50 mm thickness carriers a fluid at a pressure of 5 MN/m². The maximum circumferential stress will be:
(a) 13 MN/m²
(b) 8 MN/m²
(c) 5 MN/m²
(d) none of the above

7. A hollow shaft has an external diameter of 300 mm and an internal diameter of 150 mm. The ratio of strength with that of a solid shaft of the same weight per unit length and materials is:
(a) 1.0
(b) 1/1.44
(c) 1.44
(d) None of the above

8. In case of plane stress problems
(a) σz = 0
(b) τxz = 0
(c) τyz = 0
(d) All of the above

9. Mild steel is
(a) brittle material
(b) ductile material
(c) neither brittle nor ductile material
(d) both

10. In the determination of hardness of razor blade the method that can be used is
(a) Brinell hardness
(b) Vicker hardness 
(c) Rockwell hardness 
(d) scratch test.

Answer

1. (a) When an external force acts on a body, the body tends to undergo some deformation. If the external force is removed and the body comes back to its original shape and size (which means the deformation disappears completely), the body is known as an elastic body. This property, by virtue of which certain materials return back to their original position after the removal of the external force, is called elasticity.
The body will regain its previous shape and size only when the deformation caused by the external force, is within a certain limit. Thus there is a limiting value of force up to and within which, the deformation completely disappears on the removal of the force. The value of stress corresponding to this limiting force is known as the elastic limit of the material.

2. (b)
  • Principal stresses occur on mutually perpendicular planes.
  • Shear stresses are zero on principal planes.
  • Planes of maximum shear stress occur at 45° to the principal planes.
  • The maximum shear stress is equal to one half the difference of the principal stresses.

3. (a) 


4. (c)

5. (d)  y = M{L^2}/8EI

6. (d) {\sigma _h} = PD/2t;{\sigma _l} = PD/4t

7. (b) \frac{{{W_H}}}{{{W_S}}} = \frac{{({n^2} - 1){n^{2/3}}}}{{{{({n^4} - 1)}^{2/3}}}};n = {D_o}/{D_i} = 300/150 = 2

8. (d)

9. (b) Mild steel is a type of low carbon steel. Carbon steels are metals that contain a small percentage of carbon (max 2.1%) which enhances the properties of pure iron. The carbon content varies depending on the requirements for the steel. Low carbon steels contain carbon in the range of 0.05 to 0.25 per cent.

10. (c) When looking at knives you will often see a number in the specs with “RC” after it. This number represents the Rockwell Rating. The Rockwell rating is a scale that is used to measure the hardness of a material. The Rockwell hardness test is the industry standard for knives.

---
The study material for AMIE/B Tech/Junior Engineer exams is available at https://amiestudycircle.com 




Labels:

Comments

Post a Comment

Popular posts from this blog

Mechanics of Fluids (Solved Numerical Problems)

Numerical The surface Tension of water in contact with air at 20°C is 0.0725 N/m. The pressure inside a droplet of water is to be 0.02 N/cm² greater than the outside pressure. Calculate the diameter of the droplet of water. (7 marks) (AMIE Summer 2023) Solution Surface tension, σ = 0.0725 N/m Pressure intensity, P = 0.02 N/m 2 P = 4σ/d Hence, the Diameter of the dropd = 4 x 0.0725/200 = 1.45 mm Numerical Find the surface tension in a soap bubble of 40 mm diameter when the inside pressure is 2.5 N/m² above atmospheric pressure. (7 marks) (AMIE Summer 2023) Answer: 0.0125 N/m Numerical The pressure outside the droplet of water of diameter 0.04 mm is 10.32 N/cm² (atmospheric pressure). Calculate the pressure within the droplet if surface tension is given as 0.0725 N/m of water. (AMIE Summer 2023, 7 marks) Answer: 0.725 N/cm 2   Numerical An open lank contains water up to a depth of 2 m and above it an oil of specific gravity 0.9 for a depth of 1 m. Find the pressure intensity (i) at t...
Post a Comment
Read more

Energy Systems (Solved Numerical Problems)

Wind at 1 standard atmospheric pressure and \({15^0}C\) has velocity of 15 m/s, calculate (i) the total power density in the wind stream (ii) the maximum obtainable power density (iii) a reasonably obtainable power density (iv) total power (v) torque and axial thrust Given: turbine diameter = 120 m, and turbine operating speed = 40 rpm at maximum efficiency. Propeller type wind turbine is considered. (AMIE Winter 2023) Solution For air, the value of gas constant is R = 0.287 kJ/kg.K 1 atm = 1.01325 x 105 Pa Air density \(\rho  = \frac{P}{{RT}} = \frac{{1.01325x{{10}^5}}}{{287}}(288) = 1.226\,kg/{m^3}\) Total Power \({P_{total}} = \rho A{V_1}^3/2\) Power density \(\begin{array}{l}\frac{{{P_{total}}}}{A} = \frac{1}{2}\rho {V_1}^3\\ = \frac{1}{2}(1.226){(15)^3}\\ = 2068.87{\mkern 1mu} W/{m^2}\end{array}\) Maximum power density \(\begin{array}{l}\frac{{{P_{\max }}}}{A} = \frac{8}{{27}}\rho A{V^3}_1\\ = \frac{8}{{27}}(1.226){(15)^3}\\ = 1226{\mkern 1mu} W/{m^2}\end{array}\) Assuming eff...
Post a Comment
Read more

Design of Electrical Systems (Solved Numerical Problems)

Important note There is something wrong with this question paper. It seems that instead of "Design of Electrical Systems" the IEI has given problems from "Electrical Machines". You should raise a complaint to director_eea@ieindia.org in this regard. Numerical A 120 V DC shunt motor draws a current of 200A. The armature resistance is 0.02 ohms and the shunt field resistance is 30 ohms. Find back emf. If the lap wound armature has 90 slots with 4 conductors per slots, at what speed will the motor run when flux per pole is 0.04 Wb?​ (AMIE Summer 2023, 8 marks) Solution The back EMF (E b ) of a DC motor can be calculated using the formula: E b = V - I a R a   Given: V = 120 V I a = 200 A R a = 0.02 ohms Substituting the values into the formula: E b = 120 − 200 × 0.02 = 120 − 4​ = 116 V Now, let's calculate the speed (N) at which the motor will run using the given flux per pole (φ p ). The formula to calculate the speed of a DC motor is: N = 60×E b /(P×φ p ) Wh...
Post a Comment
Read more