Mechanics of Solids - short answer type questions from AMIE Exams (Winter 2017)

on
Write short notes on (4 marks each)

Generalised Hooke’s law

Hooke’s Law states that when a material is loaded within the elastic limit, the stress is proportional to the strain produced by the stress. This means the ratio of the stress to the corresponding strain is a constant within the elastic limit. This constant is known as Modulus of Elasticity or Modulus of Rigidity or Elastic Modulii.

Differential equation of equilibrium

The Small-Strain Stress-Strain Relations


{\varepsilon _{xx}} = \frac{{\partial {u_x}}}{{\partial x}}
{\varepsilon _{yy}} = \frac{{\partial {u_y}}}{{\partial y}}
{\varepsilon _{xy}} = \frac{1}{2}\left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right)

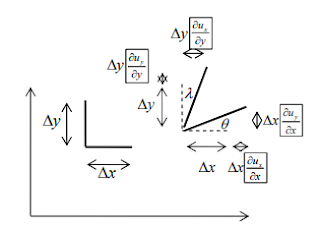
Simple Shear
{\varepsilon _{xy}} = \frac{1}{2}\left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right) = \frac{1}{2}\left( {\frac{{\partial {u_x}}}{{\partial y}}} \right)

Pure shear
{\varepsilon _{xy}} = \frac{1}{2}\left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right) = \frac{{\partial {u_x}}}{{\partial y}} = \frac{{\partial {u_y}}}{{\partial x}}

Tresca yield criteria

According to this theory, the failure of material will occur when the maximum shear stress in a material reaches the value of maximum shear stress in simple tension at the elastic limit. The maximum shear stress in the material is equal to half the difference between the maximum and minimum principal stress.

If σ₁, σ₂ and σ₃ are principal stresses at a point in material for which σt* is the principal stress in simple tension at the elastic limit, then

Max. shear stress in the material 
= Half of the difference of maximum and minimum principal stresses
= \frac{1}{2}[{\sigma _1} - {\sigma _2}]

In the case of simple tension, at the elastic limit, the principal stresses are σt*, 0, 0

Max. shear stress in simple tension at elastic limit
= \frac{1}{2}[{\sigma _t}^* - 0] = \frac{1}{2}{\sigma _t}^*

For the failure of the material
({\sigma _1} - {\sigma _3}) \ge {\sigma _t}^*

For design, the following equation should be used
({\sigma _1} - {\sigma _3}) = {\sigma _t}

Impact test

The capacity of a material to resist or absorb shock energy before it fractures is called its impact strength. The standard machine for impact testing is of the pendulum type (see figure). 


A notch is cut in the specimen, i.e. a standard test piece which struck under impact conditions by a heavyweight attached to the end of the pendulum. The test piece, i.e. specimen is held in an anvil (vice) and is broken by a single blow of the pendulum weight or hammer which is allowed to fall from a fixed starting point of a known height. The pendulum swings on after breaking the specimen and the height to which the pendulum rises on the other side are measured. 

Hardness test  

This is essentially the resistance of the surface of a material to deformation. We may note that there is no absolute scale for hardness. The commonly used tests for hardness are:
  • Brinell hardness test
  • Vickers hardness test
  • Rockwell hardness test
  • Rebound hardness test
Brinell Hardness Test
Ill this test a standard hardened steel ball of diameter D is pressed for about 10-15 seconds into the surface of the specimen by a gradually applied load P (see figure). 


The diameter of the indentation is measured after the load and ball are removed. The impression of the steel ball (indenter) so obtained, is measured to the nearest 0.2 mm with the help of a microscope.

The BHN number for some metals are
Lead: 4-8
Zinc: 25-40
Cast iron: 115-200
Nickel: 30-160
H.S.S.: 450-700

---
The study material for AMIE/B Tech/Junior Engineer exams is available at https://amiestudycircle.com 





Comments

Post a Comment