Answer the following (2 marks each)
What is Mohr’s circle?
Mohr’s circle is a graphical method of finding normal, tangential and resultant stresses on an oblique plane. Mohr’s circle will be drawn for the following cases :
- A body subjected to two mutually perpendicular principal tensile stresses of unequal intensities.
- A body subjected to two mutually perpendicular principal stresses which are unequal and unlike (i.e., one is tensile and other is compressive).
- A body subjected to two mutually perpendicular principal tensile stresses accompanied by a simple shear stress.
Consider a rectangular body subjected to two mutually perpendicular principal tensile stresses of unequal intensities. It is required to find the resultant stress on an oblique plane.
Let σ1 = Major tensile stress; σ2 = Minor tensile stress, and θ = Angle made by the oblique plane with the axis of minor tensile stress.
Then Mohr circle would be like this:
State Hooke’s law and Young’s modulus?
- Hook's law. It states that when a material is loaded within elastic limit, the stress is proportional to the strain produced by the stress. This means the ratio of the stress to the corresponding strain is a constant within the elastic limit. This constant is known as Modulus of Elasticity or Modulus of Rigidity or Elastic Modulii.
- Young’s Modulus. The ratio of tensile stress or compressive stress to the corresponding strain is a constant. This ratio is known as Young’s Modulus or Modulus of Elasticity and is denoted by E.
What is a Poisson’s ratio?
Poisson’s ratio. The ratio of lateral strain to the longitudinal strain is a constant for a given material, when the material is stressed within the elastic limit. This ratio is called Poisson’s ratio and it is generally denoted by μ.
State the principle of shear stress.
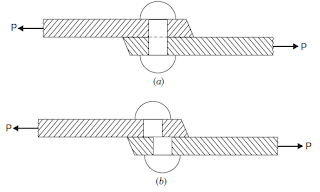
Shear Stress. The stress induced in a body, when subjected to two equal and opposite forces which are acting tangentially across the resisting section as shown in following figure as a result of which the body tends to shear off across the section, is known as shear stress.
The corresponding strain is known as shear strain. The shear stress is the stress which acts tangential to the area. It is represented by τ.
What is proof resilience?
Proof Resilience. The maximum strain energy, stored in a body, is known as proof resilience. The strain energy stored in the body will be maximum when the body is stressed upto elastic limit. Hence the proof resilience is the quantity of strain energy stored in a body when strained upto elastic limit.
Define torsional rigidity and polar moment of inertia.
Torsional rigidity
Torsional rigidity or stiffness of the shaft is defined as the product of modulus of rigidity (C) and polar moment of inertia of the shaft (J). Hence mathematically, the torsional rigidity is given as,
Torsional rigidity = C × J = TL/θ
Torsional rigidity is also defined as the torque required to produce a twist of one radian per unit length of the shaft.
Polar moment of inertia
The product of the area (or mass) and the square of the distance of the centre of gravity of the area (or mass) from an axis perpendicular to the plane of the area is known as polar moment of inertia and is represented by J.
Consider a plane area which is split up into small areas a1, a2, a3, ... etc. Let the C.G. of the small areas from a given axis be at a distance of r1, r2, r3, ... etc. Then the moment of inertia of the plane area about the given axis is given by
Explain maximum shear strain energy theory.
According to this theory, the failure of a material occurs when the total shear strain energy per unit volume in the stressed material reaches a value equal to the shear strain energy per unit volume at the elastic limit in the simple tension test.
Draw a schematic of stress-strain curve for mild steel or low carbon steel showing important points.
If tensile force is applied to a steel bar, it will have some elongation. If the force is small enough, the ratio of the stress and strain will remain proportional. This can be seen in the graph as a straight line between zero and point A – also called the limit of proportionality. If the force is greater, the material will experience elastic deformation, but the ratio of stress and strain will not be proportional. This is between points A and B, known as the elastic limit.
Beyond the elastic limit, the mild steel will experience plastic deformation. This starts the yield point – or the rolling point – which is point B, or the upper yield point. As seen in the graph, from this point on the correlation between the stress and strain is no longer on a straight trajectory. It curves from point C (lower yield point), to D (maximum ultimate stress), ending at E (fracture stress).
State few differences between tensile stress and compressive stress.
Tensile Stress. The stress induced in a body, when subjected to two equal and opposite pulls as a result of which there is an increase in length, is known as tensile stress. The ratio of increase in length to the original length is known as tensile strain. The tensile stress acts normal to the area and it pulls on the area.
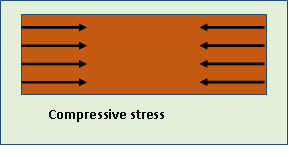
Compressive Stress. The stress induced in a body, when subjected to two equal and opposite pushes as a result of which there is a decrease in length of the body, is known as compressive stress. And the ratio of decrease in length to the original length is known as compressive strain. The compressive stress acts normal to the area and it pushes on the area.
Explain principal stress.
The planes, which have no shear stress, are known as principal planes. Hence principal planes are the planes of zero shear stress. These planes carry only normal stresses. The normal stresses, acting on a principal plane, are known as principal stresses.
---
The study material for AMIE/B Tech/Junior Engineer exams is available at https://amiestudycircle.com



Comments