Multiple choice questions: (2 x 10)
1. The dynamic viscosity is 1.2 x 10⁻⁴ Ns/m². The density is 600 kg/m³. The kinematic viscosity in m²/s is
(a) 72 x 10⁻³
(b) 20 x 10⁻⁸
(c) 7.2 x 10³
(d) 70 x 10⁶
(a) 72 x 10⁻³
(b) 20 x 10⁻⁸
(c) 7.2 x 10³
(d) 70 x 10⁶
Hint: ν = μ/ρ = 1.2 x 10-4/600
2. A horizontal cylinder half filled with fuel is having an acceleration of 10 m/s². The gravitational forces are negligible. The free surface of the liquid will be
(a) horizontal
(b) slopes in the direction of acceleration
(c) vertical
(d) slopes in the direction opposite of acceleration
(a) horizontal
(b) slopes in the direction of acceleration
(c) vertical
(d) slopes in the direction opposite of acceleration
Hint: As we know that if the liquid is accelerated horizontally, then the two points in the same horizontal line can’t have equal pressure. Therefore, the free surface of the liquid is inclined to the horizontal with larger depth at the rear end as the tanker is moving in the forward direction with uniform acceleration.
3. The centre of pressure of a rectangular plane with height of liquid h m from base
(a) h/2 m from bottom
(h) h/3 m from top
(c) h/3 m from bottom
(a) h/2 m from bottom
(h) h/3 m from top
(c) h/3 m from bottom
(d) can be determined only if liquid specific weight is known
Hint: For vertical plane surface: θ = 90°
h* = (IG/Ah̅) + h̅
IG = bh3/12
A = bh
Hence, h* = 2h/3
The distance of centre of pressure from base = h - 2h/3 = h/3
4. If a body is in stable equilibrium, the metacentric height should be
(a) zero
(b) positive
(c) negative
(d) depends on the fluid
(a) zero
(b) positive
(c) negative
(d) depends on the fluid
Hint:
GM > 0 (M is above G); Stable equilibrium
GM = 0 (M coinciding with G); Neutral equilibrium
GM < 0 (M is below G); Unstable equilibrium
GM = 0 (M coinciding with G); Neutral equilibrium
GM < 0 (M is below G); Unstable equilibrium
5. When a ship leaves a river and enters the sea
(a) It will rise a little
(b) It will sink a little
(c) there will be no change n the draft
(d) It will depend on the type of the ship
(a) It will rise a little
(b) It will sink a little
(c) there will be no change n the draft
(d) It will depend on the type of the ship
Hint: A ship rises a little when it enters the sea from a river. Seawater is salty, which exerts more pressure on the ship than river. Due to this, the shipping volume inside the sea decreases to balance the weight of the ship.
6. A potential function
(a) is constant along a streamline
(b) is definable if a stream function is available for the flow
(c) describe the flow if it is rotational
(d) inscribes the flow if it is irrotational
(a) is constant along a streamline
(b) is definable if a stream function is available for the flow
(c) describe the flow if it is rotational
(d) inscribes the flow if it is irrotational
Hint: Potential function will exist only if the flow is irrotational for both compressible and incompressible flow.
7. In a steady flow along a streamline at a location in the flow, the velocity head is 6 m. the pressure head is 3 m. the potential bead is 4 m. The height of hydraulic gradient line at this location will lie
(a) 13 m
(b) 9 m
(c) 10 m
(d) 7 m
(b) 9 m
(c) 10 m
(d) 7 m
Hint:
The hydraulic gradient Line represents the sum of pressure head and datum head (Potential head).
The total energy line represents the sum of pressure head, datum head, and velocity head.
The total energy line represents the sum of pressure head, datum head, and velocity head.
8. The more accurate flow measuring instrument is
(a) Orifice meter
(b) Venturi meter
(c) Flow meter
(d) Elbow meter
(a) Orifice meter
(b) Venturi meter
(c) Flow meter
(d) Elbow meter
9. Fluid velocity can be measured without disturbing the flow using
(a) Pitot tube
(b) Hot wire anemometer
(c) turbine meter
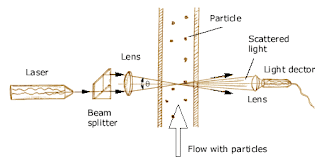
(d) Laser Doppler anemometer
(a) Pitot tube
(b) Hot wire anemometer
(c) turbine meter
(d) Laser Doppler anemometer
Hint: Laser Doppler anemometer is used to measure the velocity of a flow without disturbing the
flow. It is often used to measure turbulent velocity and also low volume flow rates. It measures
the velocity of small particles that are either naturally present in most liquid flows or are
seeded with 1 μm size particles in gas flows.
flow. It is often used to measure turbulent velocity and also low volume flow rates. It measures
the velocity of small particles that are either naturally present in most liquid flows or are
seeded with 1 μm size particles in gas flows.
10. Current meter is used to measure
(a) Pressure
(b) Velocity
(c) Density
(d) Viscosity
(a) Pressure
(b) Velocity
(c) Density
(d) Viscosity
Hint: Vane anemometers and current meters are used to measure the velocity of air and water in
larger flow fields. Hemispherical vanes are fitted on the radial arms of the vane anemometer, and cones are fitted on the current meter. Drag force on the vanes and cones when fluid moves over them causes the rotary movement of
the rotor.
larger flow fields. Hemispherical vanes are fitted on the radial arms of the vane anemometer, and cones are fitted on the current meter. Drag force on the vanes and cones when fluid moves over them causes the rotary movement of
the rotor.
---
The study material for AMIE/Junior Engineer exams is available at https://amiestudycircle.com



Comments